给定二叉树的先序遍历有多少种可能的二叉树
给定二叉树的先序遍历有多少种可能的二叉树
问题:给定二叉树的先序遍历有多少种可能的二叉树
git地址:https://github.com/944613709/HIT-Data-Structures-and-Algorithms
算法思想:
在二叉树先序遍历非递归算法中,二叉树先序遍历序列即为二叉树结点入栈顺序,而二叉树中序遍历序列即为二叉树结点出栈顺序,已知二叉树的先序遍历序列和中序遍历序列,即可确定一棵二叉树,所以问题等价于已知二叉树结点入栈顺序,有多少种可能的出栈顺序。
用队列来模拟输入,队列的输出则按照原先序列的顺序。再使用一个栈来模拟入栈和出栈,结果保存在另外一个队列
对于任意的一个元素k,要么进栈处理下一个元素,要么判断栈是否为空若不为空则进行出栈继续处理元素。当所有的元素都入栈了,k=n+1时候就可以输出队列和栈的元素,成为一个出栈序列,计数加一,再执行回溯,递归
算法步骤:
\1. 初始化栈和队列
\2. 调用OutPut_S(1);函数执行从k=1开始
(1) 如果k!=n+1,需要后续继续递归
① 将当前元素k入栈
② 处理下一个元素k+1调用OutPut_S(k+1);
③ 进行回溯到之前元素的状态利用pop(s)
④ 判断栈是非为空,如果空
\1) 栈顶元素出栈
\2) 存入队列
\3) 再次调用OutPut_S(k);处理当前元素k
\4) 出队
\5) 将此时的元素入栈,进行回溯操作,也就是抹去之前的处理,进行递归处理其他元素
(2) 如果k==n+1时,完成递归,所有元素都已经入过栈完毕,作为出口
① 打印队列元素
\1) While直到p->next!=NULL
a. 每一次printf并且p=p->next;
② 打印栈元素
\1) 利用for循环将所有元素printf
③ 并且计数利用cout++
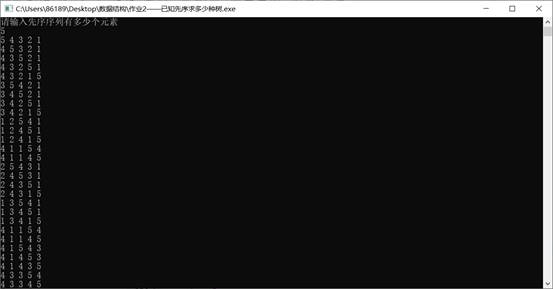
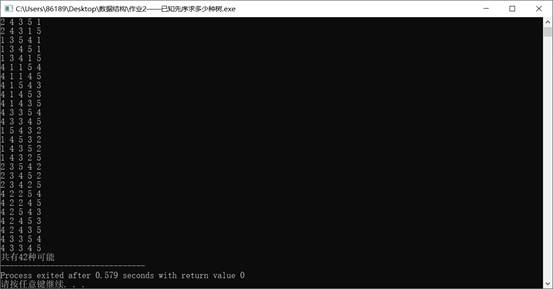
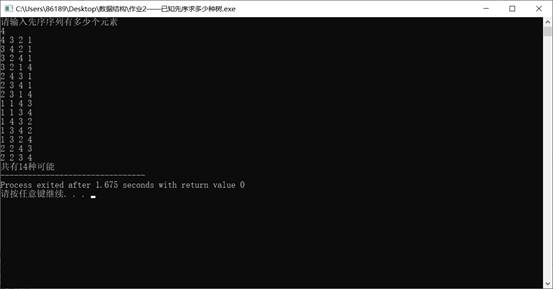
测试样例
具体代码
\#include <stdio.h>\#include <stdlib.h>\#include <string.h>\#include <stdbool.h>\#define MAX 99``
typedef struct STACK{int top;int data[MAX];}STACK;void push(STACK *s,int data){s->data[++s->top]=data;}void pop(STACK *s){s->top--;}void STACK_Initial(STACK *s){s->top=-1;}``
int top(STACK *s){return s->data[s->top];}bool Isempty(STACK *s){if(s->top==-1)
return true;else
return false;}typedef struct Qnode{int data;struct Qnode* next;}Qnode;``
typedef struct Queue{Qnode* front;Qnode* rear;}queue;void Q_Initial(queue *q){Qnode *p=malloc(sizeof(Qnode));p->next=NULL;q->front=p;q->rear=p;}void enqueue(queue *q,int k){Qnode *p=malloc(sizeof(Qnode));p->data=k;p->next=NULL;q->rear->next=p;q->rear=p;}void dequeue(queue *q){Qnode *p=q->front->next;q->front->next=p->next;free(p);if(q->front->next==NULL)
q->rear=q->front;}queue *q; //队列保存已出栈元素int n;int count=0;STACK *s;``
void OutPut_S(int k){int temp;if(k!=n+1)//当k!=n+1时候继续递归{
push(s,k);
//当前元素k入栈
OutPut_S(k+1);
//处理下一元素k+1
pop(s); //回溯至当前元素状态
if(!Isempty(s)) //当栈非空时
{
temp=top(s);
pop(s);
enqueue(q,temp);
OutPut_S(k);
dequeue(q);
push(s,temp);
}}else if(k==n+1){//当k==n+1时候结束递归
Qnode* p=q->front;
while(p->next!=NULL)
{ //将队列元素打印——已经出栈的元素
printf("%d ",p->next->data);
p=p->next;
}
int j;
//然后再打印栈的元素 ,然后回溯
for(j=s->top;j>=0;j--)
printf("%d ",s->data[j]);
count++; //计数共有几种可能
printf("\n");
return ;}``
}``
int main(){s = malloc(sizeof(STACK));STACK_Initial(s);q = malloc(sizeof(queue));Q_Initial(q);printf("请输入先序序列有多少个元素\n");
scanf("%d",&n);OutPut_S(1);printf("共有%d种可能",count);return 0;}``